ファミレスメニューを数学者が見たら、組織の課題は「ハンバーグセット」だった
(編集部注:前節から)またしても食べ物の話で恐縮だが、ファミリーレストランにはハンバーグなどの料理の種類もいくつかあり、基本の料理にいろいろなバリエーションがある。メニュー表にはこれらのバラエティに富んだ単品の料理が記載されているが、そのすべてに「ライスセット」「パンセット」「ドリンクバーセット」などのセットオプションがついていることが多い。これらのセットオプションは、それそのものが単独のメニューになっているわけではないので、単品メニューとは概念的に異なっている。
たとえば、ハンバーグ料理に「ライスセット」をつけるということは、単品メニューを定食メニューに早替わりさせる操作であり、その意味で矢印的なものだ。すなわち、それは「関手的」な操作である。
これを見るために、まずは「ハンバーグの圏」を考えてみよう(図6.3)。この図ではハンバーグ料理(=対象)が、次の三種類の矢印でつながっている。
○チーズをのせる
○各種のソースをかける
○ソースで煮込む
たとえば、ハンバーグからデミグラスハンバーグへの矢印は、もちろん「デミグラスソースをかける」という射であるし、そこからデミグラスチーズハンバーグに至る矢印は「チーズをのせる」というものである。もちろん、圏として見る場合は、各対象ごとに恒等射を考えて(追加して)、さらに矢印と矢印の合成も考える。
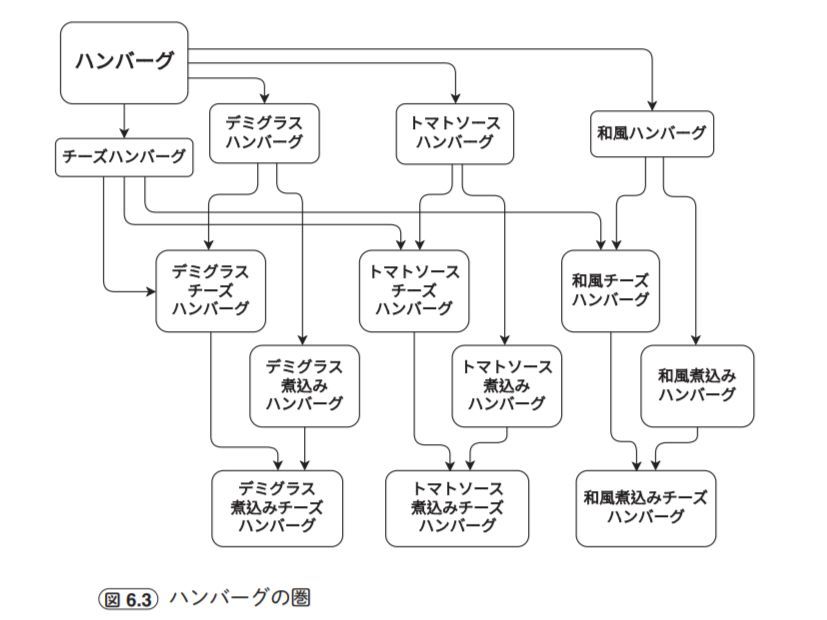
たとえば、トマトソースハンバーグからトマトソース煮込みチーズハンバーグには、トマトソースチーズハンバーグを経由した合成射がある。また、デミグラスハンバーグからデミグラス煮込みチーズハンバーグへ至る道筋は、チーズのせと煮込みのどちらを先にするかによって二通りあるが、ここでの矢印は「調理の手順」ではなくて、メニュー表に載っている料理の概念の相関関係なので、両者は等しいと考える。
「ライスセットをつけて定食化する」という関手は、ハンバーグの圏から定食の圏への関手である。それを図示したのが図6.4である。右側の点線で囲われているのは、「定食の圏」だと思ってもらいたい。ここでは左側のハンバーグの圏が「ライスセットをつける」という関手によって、そのネットワーク構造ごとゴッソリ定食の圏の中に送られているのがわかるだろう。
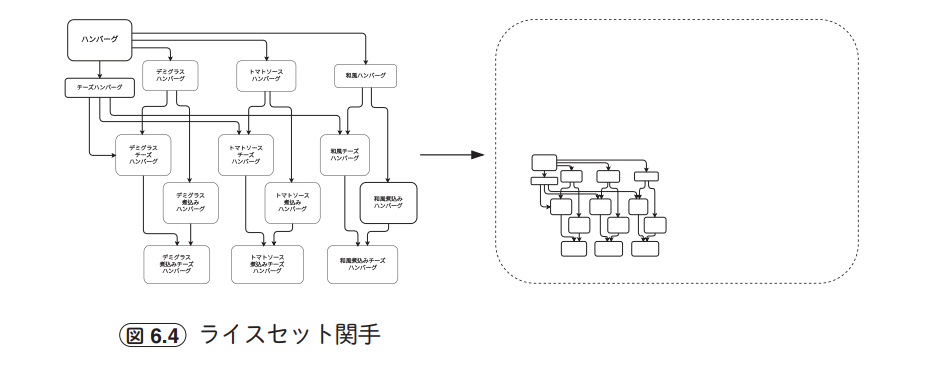
この「ライスセット関手」によって、たとえば、和風ハンバーグは和風ハンバーグ定食に送られ、和風煮込みハンバーグは和風煮込みハンバーグ定食に送られる。のみならず、当初和風ハンバーグと和風煮込みハンバーグのあいだの関係を表していた矢印(射)も、そのまま和風ハンバーグ定食から和風煮込みハンバーグ定食への矢印に送られている。ライスと味噌汁がついても、主菜であるハンバーグ同士の関係性はそのまま維持される。
ライスセット関手は、このようにして、ハンバーグの圏を定食の圏に関係付ける矢印になっている。つまり、それは圏のネットワーク構造ごとそのまま送り込むという矢印である。














































